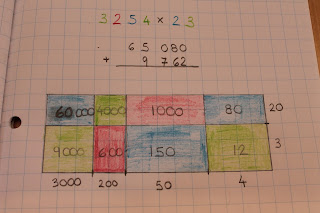Voici comment j'ai présenté la multiplication à plus d'un chiffre au multiplicateur avec la planche à clous. Cette opération a été précédemment travaillée avec le
Damier, puis le
boulier doré. Je trouve ce matériel très beau et 'parlant' visuellement. Je vous montre pourquoi... ;)
Avant toute chose, comme il s'agit d'un nouveau matériel, il faut d'abord présenter celui-ci afin que l'enfant s'y familiarise.
Nous montrons d'abord les clous dans la boîte en lui disant que les clous verts à droite représentent les unités, les bleus (à gauche des clous verts des unités) représentent les dizaines, les rouges les centaines. Puis, nous revenons aux clous verts qui représentent à présent les unités de mille, les clous bleus, les dizaines de mille et les clous rouges, les centaines de mille. Rien de nouveau, ce sont toujours les mêmes couleurs des hiérarchies avec lesquelles l'enfant est habitué de travailler, notamment avec le
Grand boulier.
L'enfant va alors s'exercer à lire des nombres sur cette planche à clous. Vous commencez à placer les clous verts des unités à droite de la planche en haut (Ici : 4).
Puis, vous placez les clous bleus à gauche des verts, puis les rouges à gauche des bleus (Le nombre représenté ici est 234). Vous demandez à l'enfant de lire ce nombre.
Ensuite, vous ajouterez les clous verts des unités de mille (en laissant un espace d'un trou entre les unités de mille et les centaines puisque nous venons de changer de hiérarchies (vous vous souvenez de la présentation des
grandes hiérarchies? ;) De cette façon, on visualise bien le changement de hiérarchie ; nous passons des unités simples (unités, dizaines, centaines) aux mille (unités de mille, dizaines de mille, centaines de mille). Sur la photo ci-dessus, l'enfant lira le nombre 3234.
Ensuite, vous demandez de lire des nombres avec des zéros (donc avec une catégorie manquante). Ici, il lira : 1602.
Finalement, vous allez reprendre les mêmes étapes graduelles dont je viens de parler, mais cette fois, vous demandez à l'enfant de représenter lui-même les nombres que vous lui dictez.
Exemple : 23 Exemple : 3204
Lorsque l'enfant est à l'aise, nous pouvons lui présenter la multiplication avec deux chiffres au multiplicateur.
Ici, nous allons effectuer la multiplication 3254 x 23.
D'abord, nous plaçons de petits billets pour représenter notre équation sur la planche à clous (3254) (23) (X ; le signe de la multiplication :). En bas, nous plaçons le multiplicande (3254) dont les clous seront placés horizontalement. À droite, nous plaçons le multiplicateur (23) dont les clous seront placés verticalement (voir photo ci-dessus). J'ai choisi de placer le multiplicande à l'horizontal en bas et le multiplicateur à la verticale à droite afin de rester cohérent avec la façon dont nous placions les nombres sur le damier (le multiplicande était en bas à l'horizontal et le multiplicateur à droite à la verticale), d'autant qu'ensuite je vous montre cela graphiquement (tout cela doit rester cohérent visuellement pour mieux comprendre et voir ;).

Nous allons donc placer les clous qui correspondent à notre multiplication à effectuer 3254 x 23 (voir photo ci-dessus). Donc, horizontalement, nous plaçons le multiplicande (3254) ; d'abord 4 clous verts des unités. Ensuite, à gauche de ces clous verts, nous plaçons 5 clous des dizaines, puis 2 clous des centaines et finalement 3 clous représentant les unités de mille. Puis, verticalement, nous plaçons le multiplicateur (23) ; d'abord 3 clous verts des unités et 2 clous bleus des dizaines
Nous commençons donc la multiplication. D'abord, nous multiplions les unités, comme toujours lorsqu'on multiplie. Pour vous aider à suivre, j'ai placé des crayons vis-à-vis les chiffres qui sont multipliés au fur et à mesure. Donc, sur la photo ci-dessus, nous multiplions une unité (clou vert) par une unité (clou vert), donc 1 x 1 = 1. Nous plaçons donc un clou vert d'unité à l'intersection comme sur la photo ci-dessus pour représenter la réponse 1.
Nous poursuivons horizontalement avec encore une fois 1 x 1 = 1.
Ainsi de suite jusqu'à ce que la première rangée des unités soient complète.
Je monte le crayon d'une rangée vers le haut sur le multiplicateur (23). Il s'agit encore d'une unité (clou vert). Nous continuons donc les multiplications des unités pour ce deuxième clou vert qui représente la deuxième unité du multiplicateur (23) (il y en a trois en tout). Encore une fois, nous avons 1 x 1 = 1, donc nous plaçons un autre clou vert à l'intersection.
Nous complétons ainsi cette autre rangée. 1 x 1 = 1 ; 1 x 1 = 1 et encore 1 x 1 = 1.
Nous complétons avec la dernière unité du multiplicateur (23). Ci-dessus, nous voyons illustrer 1 x 1 = 1 (nous plaçons un clou vert à l'intersection).
Etc, jusqu'à ce que la dernière rangée de clous verts soient complète (1 x 1 = 1 ; 1 x 1 = 1 ; 1 x 1 = 1).
Note : nous obtenons un rectangle de 12 clous verts ; cela correspond à la multiplication 3 x 4 (unité x unité) de notre opération 3254 x 23. Vous verrez que lorsqu'on multiplie, nous obtenons toujours des rectangles. ;) C'est normal puisqu'une multiplication c'est une addition répétée d'un même nombre. Ici, 3 x 4, c'est 3 fois le 4 ou 4 prit 3 fois. Cela vous rappelle-t-il quelque chose? Au besoin, référez-vous à mes articles précédents sur la mémorisation de la multiplication ici et ici. Vous verrez des rectangles, des rectangles et encore des rectangles!!! ;) Ou des carrés pour les nombres carrés, mais bon, un carré, c'est un rectangle, mais dont les quatre côtés sont égaux. ;)
Comme lorsque nous effectuons une multiplication sur papier, nous allons maintenant multiplier les unités du multiplicateur avec les dizaines du multiplicande (3254 x 23). Nous n'expliquons pas cela à l'enfant, mais c'est simplement pour vous montrer comment cela nous mène tranquillement vers l'abstraction complète (faire des calculs sur papier sans matériel).
Donc, ici (photo ci-dessus), les crayons montre que l'on multiplie une unité par une dizaine. 1 x 10 = 10 (unité x dizaine = dizaine). Nous allons donc placer un clou bleu représentant les dizaines à cette intersection.
Nous poursuivons la rangée : 1 x 10 = 10 ; 1 x 10 = 10 ; 1 x 10 = 10 et 1 x 10 = 10 en plaçant des clous bleus à chaque intersection.
Nous poursuivons avec la deuxième unité de notre multiplicateur (à droite à la verticale) qui sera multipliée avec chaque dizaine du multiplicande (en bas à l'horizontal). 1 x 10 = 10 ; 1 x 10 = 10 ; 1 x 10 = 10 ; 1 x 10 = 10 et 1 x 10 = 10.
Finalement, il nous reste la troisième unité des multiplicateurs (il y a 3 unités dans 23) que l'on multiplie avec chacune des dizaines du multiplicande : 1 x 10 = 10 ; 1 x 10 = 10 ; 1 x 10 = 10 ; 1 x 10 = 10 et 1 x 10 = 10. Voilà, nous obtenons un rectangle de 15 clous bleus. Cela correspond à la multiplication 3 x 50 = 150 ; les unités du multiplicateur fois les dizaines du multiplicande (3254 x 23).
Nous allons donc passer à la multiplication des unités du multiplicateur par les centaines du multiplicande (exactement comme nous le faisons lorsque nous effectuons ce calcul à la main). ;) Donc lorsque nous multiplions des unités par des centaines, nous obtenons des centaines (1 x 100 = 100). Nous allons donc placer un clou rouge aux intersections unités X centaines. Encore une fois, nous commençons par la première rangée pour multiplier la première unité du multiplicateur avec chacune des deux centaines du multiplicande. 1 x 100 = 100 et 1 x 100 = 100.
Puis, nous effectuons la même chose avec la deuxième unité du multiplicateur : 1 x 100 = 100 et 1 x 100 = 100.
Finalement, encore la même chose avec la troisième et dernière unité du multiplicateur (23). 1 x 100 = 100 et 1 x 100 = 100. Nous obtenons alors un rectangle de 6 clous rouges. Cela correspond à la multiplication 3 x 200 = 600 de notre opération 3254 x 23.

Nous allons à présent multiplier les unités du multiplicateur avec les unités de mille du multiplicande. Des unités multipliées par des unités de mille cela donne des unités de mille, donc 1 x 1000 = 1000. Nous placerons des perles vertes représentant les unités de mille à l'intersection des multiplications unités x unités de mille. Sur la photo ci-dessus, je les aie tous placé ; je crois que vous avez compris. Bah! J'espère! ;) Donc, j'ai effectué 1 x 1000 = 1000 ; 1 x 1000 = 1000 et 1 x 1000 = 1000 ; puis encore 1 x 1000 = 1000 ; 1 x 1000 = 1000 et 1 x 1000 = 1000 pour la deuxième rangée (multiplication avec la deuxième unité du multiplicateur. Finalement, 1 x 1000 = 1000 ; 1 x 1000 = 1000 et 1 x 1000 = 1000 pour la troisième rangée (multiplication de la troisième et dernière unité du multiplicateur (23). Nous obtenons alors un rectangle de 9 clous verts d'unités de mille, donc 9000. Cela correspond à la multiplication 3 x 3000 = 9000 de notre équation (3254 x 23).
Maintenant que nous avons multiplié les unités du multiplicateur avec chacune des catégories du multiplicande, nous allons multiplier les dizaines du multiplicateur avec toutes les catégories du multiplicande. Je vous dis, c'est pareil que lorsqu'on fait une multiplication sur papier!!!!! ;) Pour l'opération 3254 x 23 ; nous avons d'abord fait 3 x 4 ; 3 x 50 ; 3 x 200 et 3 x 3000. Nous allons maintenant faire : 20 x 4 ; 20 x 50 ; 20 x 200 et 20 x 3000.
Donc ici, je pointe la première multiplication de la première dizaine du multiplicateur avec la première unité du multiplicande. Une dizaine multipliée par une unité, cela donne une dizaine (10 x 1 = 10). Nous plaçons donc un clou bleu à l'intersection.
Nous poursuivons ainsi en multipliant la première dizaine du multiplicateur avec toute les unités du multiplicande, donc 10 x 1 = 10 ; 10 x 1 = 10 ; 10 x 1 = 10 et 10 x 1 = 10. Voilà quatre nouveaux clous bleus!
Au tour de la deuxième dizaine du multiplicateur (23) d'être multipliée avec toutes les unités du multiplicateur : 10 x 1 = 10 ; 10 x 1 = 10 ; 10 x 1 = 10 et 10 x 1 = 10. Voilà! Nous obtenons un nouveau rectangle bleu composé de 8 clous bleus. Cela correspond bel et bien à la multiplication 20 x 4 = 80 de notre opération 3254 x 23.
Nous poursuivons en multipliant les dizaines de notre multiplicateur par les dizaines de notre multiplicande. Des dizaines multipliées par des dizaines, cela donne des centaines (10 x 10 = 100, donc nous poserons des clous rouges aux intersections de ces multiplications.
Donc, sur la photo ci-dessus, nous voyons que la première dizaine du multiplicateur a été multipliée avec les cinq centaines du multiplicande. 10 x 10 = 100 ; 10 x 10 = 100 ; 10 x 10 = 100 ; 10 x 10 = 100 et 10 x 10 = 100. Cela nous donne une première rangée de clous rouges.
Nous poursuivons en multipliant la deuxième et dernière dizaine du multiplicateur (23) avec les cinq dizaines du multiplicande (3254). 10 x 10 = 100 ; 10 x 10 = 100 ; 10 x 10 = 100 ; 10 x 10 = 100 et 10 x 10 = 100. Voilà un autre rectangle rouge ; celui-ci se compose de 10 clous rouges correspondant à la multiplication 20 x 50 = 1000 de notre opération 3254 x 23.
Nous voilà rendu à multiplier les dizaines du multiplicateur par les centaines du multiplicande. Des dizaines multipliées par des centaines, cela donne des unités de mille (10 x 100 = 1000. Nous allons donc placer des clous verts à l'intersection de ces multiplications.
Je crois que je peux accélérer un peu... donc ici nous avons effectué 10 x 100 et 10 x 100, puis une autre fois 10 x 100 et 10 x 100. Nous obtenons alors 4 clous verts qui représentent le nombre 4000. C'est bel et bien le résultat de 20 x 200 de notre opération 3254 x 23.


Finalement, nous terminons en multipliant les dizaines de notre multiplicateur avec les unités de mille de notre multiplicande. Des dizaines multipliées par des unités de mille, cela donne des dizaines de mille (10 x 1000 = 10 000). Nous placerons donc des clous bleus à l'intersection de ces multiplications. Donc, sur la photo ci-dessus, j'ai commencé par effectuer 10 x 1000 ; 10 x 1000 et 10 x 1000 ; puis encore 10 x 1000, 10 x 1000 et 10 x 1000 (pour la deuxième rangée de clous bleus qui correspond à la multiplication de la deuxième dizaine du multiplicateur (23) avec les trois unités de mille du multiplicande (3254). Nous obtenons alors un rectangle de 6 clous bleus qui représentent des dizaines de mille, donc 60 000. Cela correspond effectivement à la multiplication des dizaines du multiplicateur (23) avec les unités de mille du multiplicande (3254), donc 20 x 3000 = 60 000.
Pour lire notre résultat, nous retirons les clous de notre opération.
On rassemble ensuite les clous de même valeur. Donc les clous verts des unités ensemble, les bleus des dizaines ensemble, les rouges de centaines ensemble, les verts des unités de mille ensemble (attention de ne pas les mêler avec les verts des unités) et les bleus de dizaines de mille (à ne pas mêler avec les bleus des dizaines).
Sur la photo ci-dessus, j'ai seulement commencé à ressembler les clous.
Remarquez ici que nous rassemblons les rectangles de même valeur ensemble. Les deux rectangles bleus ensemble ; les deux rectangles rouges ensemble ; les deux rectangles verts ensemble... Ceci représente le moment où nous additionnons le résultat de la multiplication des unités du multiplicateur par le résultat des dizaines du multiplicateur. Pour mieux comprendre :
3254
x 23
-------- Donc, cela représente 9762 + 65 080.
9762
+65 080
Ce rassemblement des catégories de même valeur correspond exactement à ce que nous faisions avec le Damier de la multiplication lorsque nous rassemblions les barrettes de perles colorées en en descendant les diagonales).
Voici donc toutes les clous rassemblés. Nous commençons par compter les unités et effectuons les changes lorsque cela est nécessaire. Dès que nous arrivons à 10, nous effectuons un change.
Donc ici, j'ai compté 10 clous verts des unités que je change pour une dizaine (clou bleu). Voir la photo ci-dessus.
Il reste alors deux unités et j'ai maintenant une dizaine supplémentaire suite au change.
Même chose pour les dizaines que nous changeons en centaines lorsque nous en avons dix. Ici, nous avons changé deux fois 10 dizaines, donc nous avons maintenant 2 centaines supplémentaires. On suit la même procédure avec toutes les catégories.
Finalement, nous plaçons les perles du résultat en ligne et nous le lisons : 74 842
Voici à présent cette multiplication représentée et calculée graphiquement. Je me devais d'en parler, je trouve cela trop génial et vraiment joli.
Nous reprenons donc notre multiplication 3254 x 23.

Nous comptons 4 carrés vers la gauche pour les 4 unités du multiplicande en traçant une ligne, puis en laissant un petit trait vertical pour les délimiter. Nous écrivons sous cette ligne 4. Puis, nous poursuivons à tracer une ligne vers la gauche en comptant 5 carrés pour les 5 dizaines du multiplicande. Nous écrivons sous cette ligne 50 et nous délimitons encore par un petit trait vertical. Nous poursuivons de la même façon pour les 2 centaines (200) et les 3 unités de mille du multiplicande (3000). Voici pour la ligne horizontale. Ensuite, nous passons à la représentation du multiplicateur (23) par une ligne qui monte verticalement à droite (même principe que lorsqu'on représentait ces nombres avec les clous sur la planche. Donc nous comptons 3 carrés vers le haut, puis nous délimitons les unités du multiplicateur par un petit trait. Nous écrivons 3 à côté de la ligne. Finalement, nous comptons 2 carrés vers le haut pour représenter les dizaines du multiplicateur et nous écrivons 20.

Nous relions ensuite tous ces petits traits comme sur la photo ci-dessus.
Nous sommes prêts à multiplier.
Nous commençons d'abord par les unités : 3 x 4 = 12 (calcul que j'écris en bas). Des unités multipliées par des unités, cela donne des unités, donc nous allons colorier ce rectangle en vert puisque vert est la couleur des unités. À l'intérieur de ce rectangle vert j'écris la réponse : 12.
Nous poursuivons avec les unités multipliées par les dizaines : 3 x 50 = 150. Des unités multipliées par des dizaines, cela donne des dizaines; nous allons donc colorier ce rectangle en bleu puisque bleu est la couleur des dizaines.
Nous passons donc aux unités multipliées par des centaines : 3 x 200 = 600. Unité x centaine = centaine, donc le rectangle sera colorié en rouge puisque rouge est la couleur des centaines.
Ici, nous avons calculé 3 x 3000 = 9000. Des unités multipliées par des unités de mille donnent des unités de mille ; le rectangle est donc colorié en vert puisque vert est la couleur des unités de mille.
Nous passons à la multiplication des dizaines du multiplicateur. D'abord les dizaines du multiplicateur multipliées avec les unités du multiplicande. 20 x 4 = 80. Des dizaines multipliées par des unités, cela donne des dizaines, donc nous colorions le rectangle qui représente la surface de cette multiplication en bleu.
Ensuite, 20 x 50 = 1000. Des dizaines multipliées par des dizaines, cela donne des centaines, donc nous allons colorier ce rectangle en rouge.
Ensuite, 20 x 200 = 4000. Des dizaines multipliées par des centaines, cela donne des unités de mille, donc ce rectangle sera colorié en vert.
Finalement, 20 x 3000 = 60 000. Des dizaines multipliées par des unités de mille, cela donne des dizaines de mille, donc ce rectangle sera colorié en bleu (couleur des dizaines de mille... vu avec le
matériel des grandes hiérarchies). J'ai placé à droite ci-dessus, la photo de cette même multiplication, mais avec les clous. On retrouve exactement la même configuration de rectangle. ;)
Nous additionnons ensuite la rangée du haut avec celle du bas comme nous le faisons lorsque nous calculons à la main. Sur la rangée du haut, nous avons donc 60 000, 4000, 1000, 80 que l'on additionne ensemble ; cela fait 65 080. Sur la rangée du bas, nous avons 9000, 600, 150, 12 que l'on additionne ensemble ; cela fait 9762. Nous allons donc additionner la rangée du haut avec la rangée du bas. Voir cette addition en haut sur la photo ci-dessus.
Résultat : 74 842. Ainsi représenté graphiquement, il est facile de visualiser que faire une multiplication correspond à calculer une surface. Génial n'est-ce pas? ;)
Note : Pour ceux qui n'ont pas la planche à clous, pas de panique, nous pouvons effectuer la même chose, mais avec les timbres. ;) Je vous montrerai, mais évidemment, cela demande plus de précision afin que les timbres restent droit. ;) Ou alors, vous faites comme moi et vous demandez que les cadeaux des enfants soient donnés une partie en argent pour l'achat de matériel pédagogique. ;) Les enfants reçoivent des jouets, mais moins, donc nous sommes moins submergés et ils ont du beau matériel à manipuler pour la classe. Donc, oui, le matériel Montessori est cher, et cela nous est impossible de se le permettre avec le seul salaire de mon conjoint, mais si à chaque Fête d'enfants et à Noël, vous demandez un peu d'argent pour cela + les retours d'impôt, et ce, pendant plusieurs années, vous pouvez y arriver. ;) C'est le petit truc que j'ai utilisé pendant 4 ans, donc avant la leucémie de Coralie. ;)
Donc, voici comment faire avec les timbres. Ceci étant une initiative personnelle. Si vous avez une planche à clous, il n'est pas nécessaire de faire cela. ;) Simplement, visuellement, nous voyons encore davantage le lien avec la multiplication 'graphique' que je viens de vous montrer.
Puisqu'il s'agit exactement de la même multiplication qu'avec la planche à clous expliquée plus haut, je vous laisse donc comprendre en photos seulement. Au besoin, référez-vous aux photos de la planche à clous ; c'est exactement pareil. ;) Note : pour représenter le multiplicande et le multiplicateur, j'ai simplement retourné les timbres à l'envers (ainsi, on ne se mêle pas avec les résultats des calculs).
Note : j'ai placé ici les timbres bleus à l'envers parce qu'il n'y a pas de dizaines de mille dans la boîte des timbres. ;) Donc, soit vous vous limitez à des multiplications dont le résultat est inférieur à 10 000 ou vous les tournez comme ici. ;) Cela ne cause pas de problème puisque, de toute façon, les clous de la planche à clous n'ont pas de nombre écrit dessus puisque nous sommes à un degré d'abstraction supérieur.
Encore une fois, la belle correspondance avec le graphique de la multiplication que nous avons effectué plus haut. ;) Cette alternance de couleur, vous rappellera également la grande planche du
damier de la multiplication. ;)
Euryale nous présentait d'ailleurs la multiplication avec le damier + la multiplication graphique
ici. Puis, j'ai lu
ceci en anglais (complètement en bas). J'ai trouvé cela encore plus simple ainsi et j'aimais bien le fait de voir les réponses d'inscrites sur chaque rectangle. ;) Voilà! Avec tous ces liens d'un matériel à l'autre, vous comprenez mieux toute l'intelligence et la cohérence de ce matériel. ;) Moi, ça me fascine! ;)
Finalement, je termine avec les changes pour le calcul de la réponse.
74 842 (Oups! J'ai été un peu vite lors des changes ; j'ai oublié un timbre de 1000 sur la photo. ;)
Voilà que se termine cet article très long qui traînait depuis TRÈS longtemps en brouillon sur mon blog. C'est extrêmement long écrire de tels articles ; vous n'avez pas idée. Juste le relire une fois pour le corriger a été très long... Habituellement, je le relis plus d'une fois, mais vous me pardonnerez si je ne l'ai pas fait cette fois. Je tiens à publier ces articles déjà écrit, même si c'est pas parfait puisqu'ils pourront être utiles même s'ils restent quelques coquilles, je crois... j'espère... ;).